In task B14 from the exam in mathematics, it is required to find the smallest or largest value of a function of one variable. This is a rather trivial task from mathematical analysis, and it is for this reason that every graduate can and should learn to solve it normally. high school... Let us analyze several examples that schoolchildren solved during the diagnostic work in mathematics, which took place in Moscow on December 7, 2011.
Depending on the interval over which you want to find the maximum or minimum value of the function, one of the following standard algorithms is used to solve this problem.
I. Algorithm for finding the largest or smallest value of a function on a segment:
- Find the derivative of the function.
- Select from the points suspicious of an extremum, those that belong to the given segment and the domain of the function.
- Calculate values functions(not derivative!) at these points.
- Among the obtained values, choose the largest or the smallest, it will be the desired one.
Example 1. Find smallest value functions
y = x 3 – 18x 2 + 81x+ 23 on the segment.
Solution: we act according to the algorithm for finding the smallest value of a function on a segment:
- The scope of the function is not limited: D (y) = R.
- The derivative of the function is: y ’ = 3x 2 – 36x+ 81. The domain of definition of the derivative of a function is also not limited: D (y ') = R.
- Derivative zeros: y ’ = 3x 2 – 36x+ 81 = 0, so x 2 – 12x+ 27 = 0, whence x= 3 and x= 9, our interval includes only x= 9 (one point suspicious of an extremum).
- Find the value of the function at a point suspicious of an extremum and at the edges of the interval. For the convenience of calculations, we represent the function in the form: y = x 3 – 18x 2 + 81x + 23 = x(x-9) 2 +23:
- y(8) = 8 (8-9) 2 +23 = 31;
- y(9) = 9 (9-9) 2 +23 = 23;
- y(13) = 13 (13-9) 2 +23 = 231.
So, of the obtained values, the smallest is 23. Answer: 23.
II. Algorithm for finding the largest or smallest function value:
- Find the domain of the function.
- Find the derivative of the function.
- Determine points suspicious of an extremum (those points at which the derivative of the function vanishes, and points at which there is no two-sided finite derivative).
- Mark these points and the domain of the function on the number line and determine the signs derivative(not functions!) on the resulting intervals.
- Define values functions(not the derivative!) at the minimum points (those points at which the sign of the derivative changes from minus to plus), the smallest of these values will be the smallest value of the function. If there are no minimum points, then the function does not have the smallest value.
- Define values functions(not the derivative!) at the maximum points (those points at which the sign of the derivative changes from plus to minus), the largest of these values will be the largest value of the function. If there are no maximum points, then the function has no maximum value.
Example 2. Find the largest value of the function.
Let the function y =f(NS) is continuous on the segment [ a, b]. As you know, such a function on this segment reaches the largest and the smallest values. The function can take these values either at the inner point of the segment [ a, b], or on the border of the segment.
To find the largest and smallest values of the function on the segment [ a, b] necessary:
1) find the critical points of the function in the interval ( a, b);
2) calculate the values of the function at the found critical points;
3) calculate the values of the function at the ends of the segment, that is, for x=a and x = b;
4) choose the largest and the smallest of all the calculated values of the function.
Example. Find Largest and Smallest Function Values
on the segment.
Find critical points:
These points lie inside the line segment; y(1) = ‒ 3; y(2) = ‒ 4; y(0) = ‒ 8; y(3) = 1;
at the point x= 3 and at the point x= 0.
Investigation of the function for convexity and inflection point.
Function y = f (x) called convex up in between (a, b) if its graph lies under the tangent drawn at any point of this interval, and is called convex down (concave) if its graph lies above the tangent line.
The point, upon passing through which the convexity is replaced by concavity, or vice versa, is called inflection point.
Study algorithm for convexity and inflection point:
1. Find the critical points of the second kind, that is, the points at which the second derivative is zero or does not exist.
2. Draw critical points on the number line, dividing it into intervals. Find the sign of the second derivative at each interval; if, then the function is convex upward; if, then the function is convex downward.
3. If, when passing through a critical point of the second kind, changes sign and at this point the second derivative is equal to zero, then this point is the abscissa of the inflection point. Find her ordinate.


Asymptotes of the graph of a function. Investigation of the function for asymptotes.
Definition. The asymptote of the graph of a function is called straight, which has the property that the distance from any point on the graph to this straight line tends to zero with an unlimited distance from the origin of the graph point.

There are three types of asymptotes: vertical, horizontal and inclined.
Definition. The straight line is called vertical asymptote function graphics y = f (x) if at least one of the one-sided limits of the function at this point is equal to infinity, that is
![]()
where is the discontinuity point of the function, that is, it does not belong to the domain of definition.
Example.
D ( y) = (‒ ∞; 2) (2; + ∞)
x= 2 - break point.
Definition. Straight y =A called horizontal asymptote function graphics y = f (x) at, if
Example.
|
x | |||
|
y |

Definition. Straight y =kx +b (k≠ 0) is called oblique asymptote function graphics y = f (x) at, where
![]()
General scheme for the study of functions and plotting.
Function research algorithmy = f (x) :
1. Find the domain of the function D (y).
2. Find (if possible) the points of intersection of the graph with the coordinate axes (for x= 0 and for y = 0).
3. Investigate for evenness and oddness of the function ( y (‒ x) = y (x) ‒ parity; y(‒ x) = ‒ y (x) ‒ odd).
4. Find the asymptotes of the graph of the function.
5. Find the intervals of monotonicity of the function.
6. Find the extrema of the function.
7. Find the intervals of convexity (concavity) and inflection points of the graph of the function.
8. Based on the research carried out, build a graph of the function.
Example. Examine the function and graph it.
1) D (y) =
x= 4 - break point.
2) When x = 0,
(0; - 5) - intersection point with oy.
At y = 0,
3)
y(‒
x)=
![]() function general view(neither even nor odd).
function general view(neither even nor odd).
4) Investigate for asymptotes.
a) vertical
b) horizontal

c) find oblique asymptotes where

‒ Oblique asymptote equation
5) In this equation, it is not required to find the intervals of monotonicity of the function.
6)![]()
![]()
![]()
These critical points split the entire domain of the function on the interval (˗∞; ˗2), (˗2; 4), (4; 10) and (10; + ∞). It is convenient to present the results obtained in the form of the following table:
|
no extras |
The table shows that the point NS= ‒2 ‒ maximum point, at the point NS= 4 ‒ no extremum, NS= 10 ‒ minimum point.
Substitute the value (- 3) into the equation:
9 + 24 ‒ 20 > 0
25 ‒ 40 ‒ 20 < 0
121 ‒ 88 ‒ 20 > 0
The maximum of this function is ![]()
(- 2; - 4) - maximum extreme.
The minimum of this function is ![]()
(10; 20) - minimum extremum.
7) investigate for convexity and inflection point of the graph of the function

In practice, it is quite common to use a derivative in order to calculate the largest and smallest value of a function. We perform this action when we figure out how to minimize costs, increase profits, calculate the optimal load on production, etc., that is, in those cases when it is necessary to determine the optimal value of any parameter. To solve such problems correctly, you need to understand well what the largest and smallest values of a function are.
We usually define these values within a certain interval x, which may in turn correspond to the entire domain of the function or part of it. It can be like a segment [a; b] and an open interval (a; b), (a; b], [a; b), an infinite interval (a; b), (a; b], [a; b) or an infinite interval - ∞; a, (- ∞; a], [a; + ∞), (- ∞; + ∞).
In this article we will tell you how the largest and smallest value of an explicitly given function with one variable y = f (x) y = f (x) is calculated.
Basic definitions
Let's start, as always, with the formulation of basic definitions.
Definition 1
The largest value of the function y = f (x) on some interval x is the value maxy = f (x 0) x ∈ X, which for any value xx ∈ X, x ≠ x 0 makes the inequality f (x) ≤ f (x 0).
Definition 2
The smallest value of the function y = f (x) on some interval x is the value minx ∈ X y = f (x 0), which for any value x ∈ X, x ≠ x 0 makes the inequality f (X f (x) ≥ f (x 0).
These definitions are fairly obvious. It can be even simpler to say this: the largest value of a function is its largest value in a known interval at x 0, and the smallest is the smallest accepted value in the same interval at x 0.
Definition 3
Stationary points are those values of the argument of a function at which its derivative vanishes.
Why do we need to know what stationary points are? To answer this question, one must recall Fermat's theorem. It follows from it that a stationary point is a point at which the extremum of the differentiable function is located (i.e., its local minimum or maximum). Consequently, the function will take the smallest or largest value over a certain interval exactly at one of the stationary points.
Another function can take the largest or smallest value at those points at which the function itself is definite, and its first derivative does not exist.
The first question that arises when studying this topic: in all cases, can we determine the largest or smallest value of a function on a given segment? No, we cannot do this when the boundaries of a given interval coincide with the boundaries of the domain of definition, or if we are dealing with an infinite interval. It also happens that a function in a given segment or at infinity will take infinitely small or infinitely large values. In these cases, it is not possible to determine the highest and / or lowest value.
These points will become clearer after being shown on the graphs:
The first figure shows us a function that takes the largest and smallest values (m a x y and m i n y) at stationary points located on the segment [- 6; 6].
Let us examine in detail the case indicated in the second graph. Let's change the value of the segment to [1; 6] and we obtain that the largest value of the function will be achieved at a point with an abscissa in the right border of the interval, and the smallest - at a stationary point.
In the third figure, the abscissas of the points represent the boundary points of the segment [- 3; 2]. They correspond to the highest and lowest values of the given function.

Now let's look at the fourth figure. In it, the function takes m a x y (the largest value) and m i n y (the smallest value) at stationary points on the open interval (- 6; 6).
If we take the interval [1; 6), then we can say that the smallest value of the function on it will be achieved at a stationary point. The greatest value will be unknown to us. The function could take its largest value at x equal to 6 if x = 6 belonged to the interval. It is this case that is depicted in graph 5.
On graph 6, this function acquires the smallest value at the right border of the interval (- 3; 2], and we cannot draw definite conclusions about the largest value.

In Figure 7, we see that the function will have m a x y at a stationary point with an abscissa equal to 1. The function will reach its smallest value at the border of the interval on the right side. At minus infinity, the values of the function will asymptotically approach y = 3.
If we take the interval x ∈ 2; + ∞, then we will see that the given function will take neither the smallest nor the largest value on it. If x tends to 2, then the values of the function will tend to minus infinity, since the straight line x = 2 is vertical asymptote... If the abscissa tends to plus infinity, then the values of the function will asymptotically approach y = 3. It is this case that is depicted in Figure 8.
In this subsection, we present a sequence of actions that must be performed to find the largest or smallest value of a function on a certain segment.
- First, let's find the domain of the function. Let us check whether the segment specified in the condition is included in it.
- Now let's calculate the points contained in this segment, where the first derivative does not exist. Most often they can be found in functions, the argument of which is written under the modulus sign, or in power functions, the exponent of which is a fractionally rational number.
- Next, let's find out which stationary points fall into the given segment. To do this, you need to calculate the derivative of the function, then equate it to 0 and solve the resulting equation, and then choose the appropriate roots. If we do not get any stationary points or they do not fall into the given segment, then we proceed to the next step.
- We determine what values the function will take at the given stationary points (if any), or at those points where the first derivative does not exist (if any), or we calculate the values for x = a and x = b.
- 5. We have got a series of function values, from which we now need to select the largest and the smallest. These will be the largest and smallest values of the function that we need to find.
Let's see how to correctly apply this algorithm when solving problems.
Example 1
Condition: the function y = x 3 + 4 x 2 is given. Determine its largest and smallest value on the segments [1; 4] and [- 4; - 1 ] .
Solution:
Let's start by finding the domain of this function. In this case, it will be the set of all real numbers except 0. In other words, D (y): x ∈ (- ∞; 0) ∪ 0; + ∞. Both segments specified in the condition will be inside the definition area.
Now we calculate the derivative of the function according to the rule for differentiating the fraction:
y "= x 3 + 4 x 2" = x 3 + 4 "x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 xx 4 = x 3 - 8 x 3
We learned that the derivative of the function will exist at all points of the segments [1; 4] and [- 4; - 1 ] .
Now we need to define the stationary points of the function. We do this using the equation x 3 - 8 x 3 = 0. It only has one valid root, which is 2. It will be a stationary point of the function and fall into the first segment [1; 4 ] .
We calculate the values of the function at the ends of the first segment and at a given point, i.e. for x = 1, x = 2 and x = 4:
y (1) = 1 3 + 4 1 2 = 5 y (2) = 2 3 + 4 2 2 = 3 y (4) = 4 3 + 4 4 2 = 4 1 4
We have obtained that the largest value of the function m a x y x ∈ [1; 4] = y (2) = 3 will be achieved at x = 1, and the smallest m i n y x ∈ [1; 4] = y (2) = 3 - for x = 2.
The second segment does not include any stationary points, so we need to calculate the values of the function only at the ends of the given segment:
y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3
Hence, m a x y x ∈ [- 4; - 1] = y (- 1) = 3, m i n y x ∈ [- 4; - 1] = y (- 4) = - 3 3 4.
Answer: For the segment [1; 4] - m a x y x ∈ [1; 4] = y (2) = 3, m i n y x ∈ [1; 4] = y (2) = 3, for the segment [- 4; - 1] - m a x y x ∈ [- 4; - 1] = y (- 1) = 3, m i n y x ∈ [- 4; - 1] = y (- 4) = - 3 3 4.
See the picture:

Before studying this method, we advise you to repeat how to correctly calculate the one-sided limit and the limit at infinity, as well as learn the basic methods for finding them. To find the largest and / or the smallest value of a function on an open or infinite interval, perform the following steps in sequence.
- First, you need to check whether the specified interval will be a subset of the scope of this function.
- Let us determine all points that are contained in the required interval and in which the first derivative does not exist. They are usually found in functions where the argument is enclosed in the modulus sign, and in power functions with fractionally rational exponents. If these points are absent, then you can proceed to the next step.
- Now we will determine which stationary points fall into the given interval. First, we equate the derivative to 0, solve the equation, and find suitable roots. If we do not have a single stationary point or they do not fall within the specified interval, then we immediately proceed to further actions. They are determined by the type of interval.
- If the interval is of the form [a; b), then we need to calculate the value of the function at the point x = a and the one-sided limit lim x → b - 0 f (x).
- If the interval has the form (a; b], then we need to calculate the value of the function at the point x = b and the one-sided limit lim x → a + 0 f (x).
- If the interval has the form (a; b), then we need to calculate the one-sided limits lim x → b - 0 f (x), lim x → a + 0 f (x).
- If the interval is of the form [a; + ∞), then it is necessary to calculate the value at the point x = a and the limit at plus infinity lim x → + ∞ f (x).
- If the interval looks like (- ∞; b], calculate the value at the point x = b and the limit at minus infinity lim x → - ∞ f (x).
- If - ∞; b, then we assume the one-sided limit lim x → b - 0 f (x) and the limit at minus infinity lim x → - ∞ f (x)
- If - ∞; + ∞, then we consider the limits at minus and plus infinity lim x → + ∞ f (x), lim x → - ∞ f (x).
- In the end, you need to draw a conclusion based on the obtained function values and limits. There are many possibilities here. So, if the one-sided limit is equal to minus infinity or plus infinity, then it is immediately clear that nothing can be said about the smallest and largest value of the function. Below we will analyze one typical example. Detailed descriptions will help you understand what's what. If necessary, you can return to Figures 4 - 8 in the first part of the material.
Condition: given a function y = 3 e 1 x 2 + x - 6 - 4. Calculate its highest and lowest values in the intervals - ∞; - 4, - ∞; - 3, (- 3; 1], (- 3; 2), [1; 2), 2; + ∞, [4; + ∞).
Solution
The first step is to find the domain of the function. The denominator of the fraction is square trinomial which shouldn't go to 0:
x 2 + x - 6 = 0 D = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ D (y): x ∈ (- ∞; - 3) ∪ (- 3; 2) ∪ (2; + ∞)
We got the domain of the function to which all the intervals specified in the condition belong.
Now let's differentiate the function and get:
y "= 3 e 1 x 2 + x - 6 - 4" = 3 e 1 x 2 + x - 6 "= 3 e 1 x 2 + x - 6 1 x 2 + x - 6" = = 3 · E 1 x 2 + x - 6 · 1 "· x 2 + x - 6 - 1 · x 2 + x - 6" (x 2 + x - 6) 2 = - 3 · (2 x + 1) · e 1 x 2 + x - 6 x 2 + x - 6 2
Consequently, the derivatives of the function exist over the entire domain of its definition.
Let's move on to finding stationary points. The derivative of the function vanishes at x = - 1 2. This is a stationary point located in the intervals (- 3; 1] and (- 3; 2).
We calculate the value of the function at x = - 4 for the interval (- ∞; - 4], as well as the limit at minus infinity:
y (- 4) = 3 e 1 (- 4) 2 + (- 4) - 6 - 4 = 3 e 1 6 - 4 ≈ - 0. 456 lim x → - ∞ 3 e 1 x 2 + x - 6 = 3 e 0 - 4 = - 1
Since 3 e 1 6 - 4> - 1, it means that maxyx ∈ (- ∞; - 4] = y (- 4) = 3 e 1 6 - 4. This does not allow us to unambiguously determine the smallest value of the function. We can only to conclude that there is a limitation - 1 at the bottom, since it is to this value that the function approaches asymptotically at minus infinity.
The peculiarity of the second interval is that there is not a single stationary point and not a single strict boundary in it. Therefore, we cannot calculate either the largest or the smallest value of the function. Having determined the limit at minus infinity and as the argument tends to - 3 on the left side, we will get only the range of values:
lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1
This means that the values of the function will be located in the interval - 1; + ∞
To find the largest value of the function in the third interval, we determine its value at the stationary point x = - 1 2, if x = 1. We also need to know the one-sided limit for the case when the argument tends to - 3 on the right side:
y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1. 444 y (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1. 644 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4
We have found that the function will take the greatest value at the stationary point maxyx ∈ (3; 1] = y - 1 2 = 3 e - 4 25 - 4. As for the smallest value, we cannot determine it. , Is the presence of a restriction from below to - 4.
For the interval (- 3; 2), we take the results of the previous calculation and once again calculate what the one-sided limit is equal to when tending to 2 on the left side:
y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1. 444 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4
Hence, m a x y x ∈ (- 3; 2) = y - 1 2 = 3 e - 4 25 - 4, and the smallest value cannot be determined, and the values of the function are bounded from below by the number - 4.
Based on what we got in the two previous calculations, we can assert that on the interval [1; 2) the function will take the largest value at x = 1, and it is impossible to find the smallest one.
On the interval (2; + ∞), the function will reach neither the largest nor the smallest value, i.e. it will take values from the interval - 1; + ∞.
lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1
Having calculated what the value of the function will be for x = 4, we find out that m a x y x ∈ [4; + ∞) = y (4) = 3 e 1 14 - 4, and the given function at plus infinity will asymptotically approach the line y = - 1.
Let's compare what we got in each calculation with the graph of the given function. In the figure, the asymptotes are shown with a dotted line.

That's all we wanted to tell you about finding the largest and smallest function value. The sequences of actions that we have given will help you make the necessary calculations as quickly and easily as possible. But remember that it is often useful to first find out at what intervals the function will decrease and at what intervals it will increase, after which you can draw further conclusions. This way you can more accurately determine the largest and smallest value of the function and justify the results obtained.
If you notice an error in the text, please select it and press Ctrl + Enter
The pictures below show where the function can reach its smallest and largest value. In the left figure, the smallest and largest values are fixed at the points of the local minimum and maximum of the function. In the right figure - at the ends of the line segment.

If the function y = f(x) is continuous on the segment [ a, b], then it reaches on this segment the smallest and highest values ... This, as already mentioned, can happen either in extremum points, or at the ends of the segment. Therefore, to find the smallest and maximum function values continuous on the segment [ a, b], you need to calculate its values in all critical points and at the ends of the segment, and then choose the smallest and largest of them.
Let, for example, it is required to determine the largest value of the function f(x) on the segment [ a, b]. To do this, find all its critical points lying on [ a, b] .
Critical point is called the point at which function defined, and her derivative is either zero or does not exist. Then you should calculate the values of the function at the critical points. And, finally, one should compare the values of the function at critical points and at the ends of the segment ( f(a) and f(b)). The largest of these numbers will be the largest value of the function on the segment [a, b] .
The problems of finding smallest function values .
Looking for the smallest and largest values of the function together
Example 1. Find the smallest and largest values of a function ![]() on the segment [-1, 2]
.
on the segment [-1, 2]
.
Solution. Find the derivative of this function. Let us equate the derivative to zero () and get two critical points: and. To find the smallest and largest values of a function on a given segment, it is sufficient to calculate its values at the ends of the segment and at a point, since the point does not belong to the segment [-1, 2]. These function values are as follows:,,. It follows that smallest function value(in the graph below it is marked in red), equal to -7, is reached at the right end of the segment - at the point, and the greatest(also red on the graph), equal to 9, - at the critical point.

If a function is continuous in some interval and this interval is not a segment (but is, for example, an interval; the difference between an interval and a segment: the boundary points of the interval are not included in the interval, and the boundary points of the segment are included in the segment), then among the values of the function it may not be be the smallest and the largest. So, for example, the function shown in the figure below is continuous at] -∞, + ∞ [and has no greatest value.

However, for any interval (closed, open, or infinite), the following property of continuous functions is true.
For self-checking during calculations, you can use online derivative calculator .
Example 4. Find the smallest and largest values of a function on the segment [-1, 3] .
Solution. We find the derivative of this function as the derivative of the quotient:
 .
.
We equate the derivative to zero, which gives us one critical point:. It belongs to the segment [-1, 3]. To find the smallest and largest values of a function on a given segment, we find its values at the ends of the segment and at the found critical point:

We compare these values. Conclusion: equal to -5/13, at point and the greatest value equal to 1 at the point.
We continue to search for the smallest and largest values of the function together
There are teachers who, on the topic of finding the smallest and largest values of a function, do not give students to solve examples more complicated than those just considered, that is, those in which the function is a polynomial or a fraction, the numerator and denominator of which are polynomials. But we will not limit ourselves to such examples, since among teachers there are those who like to make students think in full (table of derivatives). Therefore, the logarithm and trigonometric function will be used.
Example 8. Find the smallest and largest values of a function on the segment .
Solution. Find the derivative of this function as derivative work :
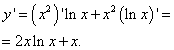
We equate the derivative to zero, which gives one critical point:. It belongs to the segment. To find the smallest and largest values of a function on a given segment, we find its values at the ends of the segment and at the found critical point:

The result of all actions: function reaches its smallest value equal to 0 at the point and at the point and the greatest value equal to e², at the point.
For self-checking during calculations, you can use online derivative calculator .
Example 9. Find the smallest and largest values of a function ![]() on the segment .
on the segment .
Solution. Find the derivative of this function:
Equating the derivative to zero:

The only critical point belongs to the line segment. To find the smallest and largest values of a function on a given segment, we find its values at the ends of the segment and at the found critical point:

Output: function reaches its smallest value equal to at the point and the greatest value, equal, at the point.
In applied extreme problems, finding the smallest (largest) values of a function, as a rule, is reduced to finding a minimum (maximum). But of greater practical interest are not the minima or maxima themselves, but those values of the argument at which they are reached. When solving applied problems, an additional difficulty arises - the compilation of functions describing the phenomenon or process under consideration.
Example 10. A tank with a capacity of 4, which has the shape of a parallelepiped with a square base and is open at the top, must be fished out with tin. How big should the tank be to cover the least amount of material?
Solution. Let be x- side of the base, h- tank height, S- its surface area without a cover, V- its volume. The surface area of the tank is expressed by the formula, i.e. is a function of two variables. To express S as a function of one variable, we will use the fact that, whence. Substituting the found expression h into the formula for S:
Let us examine this function for an extremum. It is defined and differentiable everywhere in] 0, + ∞ [, and
![]() .
.
Equate the derivative to zero () and find the critical point. In addition, for the derivative does not exist, but this value is not included in the domain of definition and therefore cannot be an extremum point. So, this is the only critical point. Let's check it for the presence of an extremum using the second sufficient criterion. Let's find the second derivative. When the second derivative is greater than zero (). Hence, at, the function reaches a minimum ![]() ... Since this minimum is the only extremum of this function, it is also its smallest value... So, the side of the base of the tank should be equal to 2 m, and its height.
... Since this minimum is the only extremum of this function, it is also its smallest value... So, the side of the base of the tank should be equal to 2 m, and its height.
For self-checking during calculations, you can use
The concept of the largest and smallest values of a function.
The concept of highest and lowest values is closely related to the concept of the critical point of a function.
Definition 1
$ x_0 $ is called a critical point of the function $ f (x) $ if:
1) $ x_0 $ - inner point of the domain of definition;
2) $ f "\ left (x_0 \ right) = 0 $ or does not exist.
Let us now introduce the definitions of the largest and smallest values of a function.
Definition 2
The function $ y = f (x) $, defined on the interval $ X $, reaches its maximum value if there is a point $ x_0 \ in X $ such that for all $ x \ in X $ the inequality
Definition 3
The function $ y = f (x) $, defined on the interval $ X $, reaches its smallest value if there is a point $ x_0 \ in X $ such that for all $ x \ in X $ the inequality
Weierstrass' theorem on a continuous function on an interval
To begin with, we introduce the concept of a continuous function on an interval:
Definition 4
A function $ f \ left (x \ right) $ is called continuous on the segment $$ if it is continuous at each point of the interval $ (a, b) $, and is also continuous on the right at the point $ x = a $ and on the left at the point $ x = b $.
Let us formulate a theorem on a continuous function on an interval.
Theorem 1
Weierstrass theorem
The function $ f \ left (x \ right) $ continuous on the segment $$ reaches its maximum and minimum value on this segment, that is, there are points $ \ alpha, \ beta \ in $ such that for all $ x \ in $ inequality $ f (\ alpha) \ le f (x) \ le f (\ beta) $.
The geometric interpretation of the theorem is shown in Figure 1.
Here the function $ f (x) $ reaches its smallest value at the point $ x = \ alpha $ and reaches its largest value at the point $ x = \ beta $.
Scheme for finding the largest and smallest values of the function $ f (x) $ on the segment $$
1) Find the derivative $ f "(x) $;
2) Find the points at which the derivative $ f "\ left (x \ right) = 0 $;
3) Find the points at which the derivative $ f "(x) $ does not exist;
4) Select from the points obtained in points 2 and 3 those that belong to the segment $$;
5) Calculate the value of the function at the points obtained in step 4, as well as at the ends of the segment $$;
6) Select the largest and smallest value from the obtained values.
Problems of finding the largest and smallest values of a function on a segment
Example 1
Find the largest and smallest value of a function on an interval: $ f (x) = (2x) ^ 3-15x ^ 2 + 36x + 1 $
Solution.
1) $ f "\ left (x \ right) = 6x ^ 2-30x + 36 $;
2) $ f "\ left (x \ right) = 0 $;
\ \ \
4) $ 2 \ in \ left, \ 3 \ in $;
5) Values:
\ \ \ \
6) The largest found value is $ 33 $, the smallest value found is $ 1 $. Thus, we get:
Answer:$ max = 33, \ min = 1 $.
Example 2
Find the largest and smallest function value on the segment: $ f \ left (x \ right) = x ^ 3-3x ^ 2-45x + 225 $
Solution.
The solution will be carried out according to the above given scheme.
1) $ f "\ left (x \ right) = 3x ^ 2-6x-45 $;
2) $ f "\ left (x \ right) = 0 $;
\ \ \
3) $ f "(x) $ exists at all points of the domain;
4) $ -3 \ notin \ left, \ 5 \ in $;
5) Values:
\ \ \
6) The largest found value is $ 225 $, the smallest value found is $ 50 $. Thus, we get:
Answer:$ max = 225, \ min = $ 50.
Example 3
Find the largest and smallest function value on the segment [-2,2]: $ f \ left (x \ right) = \ frac (x ^ 2-6x + 9) (x-1) $
Solution.
The solution will be carried out according to the above given scheme.
1) $ f "\ left (x \ right) = \ frac (\ left (2x-6 \ right) \ left (x-1 \ right) - (x ^ 2-6x + 9)) (((x- 1)) ^ 2) = \ frac (x ^ 2-2x-3) (((x-1)) ^ 2) $;
2) $ f "\ left (x \ right) = 0 $;
\ [\ frac (x ^ 2-2x-3) (((x-1)) ^ 2) = 0 \] \ \
3) $ f "(x) $ does not exist at the point $ x = 1 $
4) $ 3 \ notin \ left [-2,2 \ right], \ -1 \ in \ left [-2,2 \ right], \ 1 \ in \ left [-2,2 \ right] $, but 1 does not belong to the domain of definition;
5) Values:
\ \ \
6) The largest found value is $ 1 $, the smallest value found is $ -8 \ frac (1) (3) $. Thus, we get: \ end (enumerate)
Answer:$ max = 1, \ min == - 8 \ frac (1) (3) $.